Rakudo comes with a built-in profiler. Invoke the program with the --profiler option and
$ perl6 --profiler some_script.p6 ... output ... Writing profiler output to profile-1480712222.02931.html
That profile is an HTML file using Bootstrap and other fun things to make it look pretty. It’s not as sophisticated as something like Perl 5’s Devel::NYTProf, but it’s still pretty interesting.
Let’s write some routines to do Fibonacci numbers, which seem to be most authors’ favorite example for this sort of thing. Indeed, I used it in the “Benchmarking” chapter of Mastering Perl, but mostly to point out how wrong the simple benchmarks were.
I’ll implement it in four ways, none of which I claim to be the best:
- The recursive way you see in most examples
- A recursive fashion with memoization
- Using the sequence operator
- Using memoization with an iterative approach.
In Mastering Perl, I presented a few arguments that escape the usual discussion:
- The routine that runs fastest the first time isn’t necessarily the best
- Caching results you’ll use again eventually pays off in time
- Using less time usually means using less memory
- You improve with better algorithms instead of different syntax.
Here are some implementations in Perl 6, where I didn’t try at all to make them efficient. I merely want something to show the workings of the profiler:
sub fib_recursive ( Int $n where * >= 0 --> Int ) {
return 1 if $n < 2;
return fib_recursive( $n - 1 ) + fib_recursive( $n - 2 )
}
sub fib_recursive_memoize ( Int $n where * >= 0 --> Int ) {
state @n = ( 1, 1 );
return @n[$n] if $n < @n.elems;
return @n[$n] = fib_recursive_memoize( $n - 1 ) + fib_recursive_memoize( $n - 2 )
}
sub fib_sequence ( Int $n where * >= 0 --> Int ) {
my $seq := 1, 1, * + * ... *;
$seq[$n]
}
sub fib_memoize ( Int $n where * >= 0 --> Int ) {
state @n = ( 1, 1 );
return @n[$n] if $n < @n.elems;
for @n.elems .. $n -> $index {
@n[$index] = @n[$index-1] + @n[$index-2];
}
@n[*-1]
}
sub MAIN ( Int $n where * >= 0 --> Int ) {
for 1 .. 10 {
say fib_recursive( $n );
say fib_recursive_memoize( $n );
say fib_sequence( $n );
say fib_memoize( $n );
}
}
I run this program under the profiler, and if I’ve everything correctly, I should see the same number output several times. Or, I’ve done it wrong the same way each time.
$ perl6 --profile fib.p6 20 10946 10946 ..... 10946 10946 Writing profiler output to profile-1480712222.02931.html
If you don’t like that filename, you can choose your own:
$ perl6 --profile --profile-filename=fibonacci.html fib.p6 20 10946 10946 ..... 10946 10946 Writing profiler output to fibonacci.html
I can then look at the profiler output. Here’s a screenshot that shows the time spent in each of the subroutines:
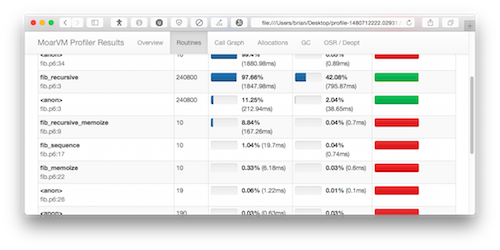
To see the rest of the report, run the program yourself!
I won’t write too much about interpreting these results, but there are several things you should think about in these sorts of comparisons.
First, test with a variety of values, especially those of vastly different orders of magnitude. The recursive solution might look really fast for small N, but it gets bad very quickly.
Second, test it several times, as I’ve done in this example. Some implementations always take the same amount of time while others get faster and faster. In a program where this level of optimization matters, you’re likely to run the interesting routine several times.
Third, consider a completely different approach than any you see here. The Fibonacci numbers aren’t going to change (neither are the values of other sequences). Why compute them again? Just look them up. (I’ll write more about this tomorrow when I use multi subs) Something like Redis can store huge lists without eating all your resources or complicating your program.

You can make fib_sequence a lot faster by using a state variable:
state @seq = 1, 1, * + * … *;
The profiler also supports JSON format, if you use .json extension on the –profile-filename= and December 2016 release will also feature SQL format.